notes on Kent’s algorithmic zoning idea
how would the community decide on setting priorities
multi layered topics
decision is multi layered
| no. | what to prioritise | option 1 | option 2 | option 3 |
| 1 | types of landuse | housing | commercial | office |
| 2 | types of housing | luxury housing | family housing | affordable housing |
-> topic 2 seems to be a subset of topic 1, if we take this fact as granted, topic 1 dominates how much affordable housing we will get after all. But topic 2 might be more contensious.
have two meetings vs one meeting altogether => you can do both
https://colab.research.google.com/drive/1E_sEWu7B3n-lBKDttaZ1_FpAtWzBSNXG#scrollTo=yN0vYIDU1yeY
elements that are important
- housing
- job
- amenities
lotka volterra model
https://en.wikipedia.org/wiki/Lotka%E2%80%93Volterra_equations
this model was used in namaph (in conjunction with CA) to simulate plant diversity, which I see that we can convert it to land use agents.
I oppose using this model for October, since this is overkill to convey the idea.
pro formas
data
cost = 1_000_000 deposit = 300_000 # this is how much you pay upfront rent = 4500 years = 15 months = 12 * years
Yield
cash flow
cf = - cost + deposit + rent * months cf
11000f
so we are not broke…
Gross rental yield
\(r\): rent \(d\): duration \(p\): value
\[ (r * d / v) * 100 \]
yeild = (rent * months / (cost - deposit)) * 100 yeild
115.71428571428572
Net rental yield
substracting the expenses from the raw gain.
\(e\): expenses
\[ {(r * d) - e } / v * 100 \]
NPV (Net Present Value)
\[ NPV()= \sum^N_{t=0} \frac{B_t}{(1 + i)^t} - \sum^N_{t=0} \frac{C_t}{(1 + i)^t} \]
\(t\) : time period \(i\) : discount rate (interest) \(N\) : total number of periods \(B\) : cash inflow \(C\) : cash outflow
positive NPV means the investment is good.
import pyxirr cf = [-cost + deposit] + [rent * 12] * years result = pyxirr.npv(0, cf) result
110000.0
IRR (Internal Rate of Return)
\[ \sum_{t=0}^{N} \frac{C_t}{(1+r)^t} = 0 \]
\(C\) : Cash flow, \(C_0\) should be negative \(r\) : interal rate of return
you set a base rate, and if the IRR is higher than that it’s a good investment.
result = pyxirr.irr(cf) * 100.00 result
1.882474875730264
Dynamic Demand Curve and program markets
memo from last meeting
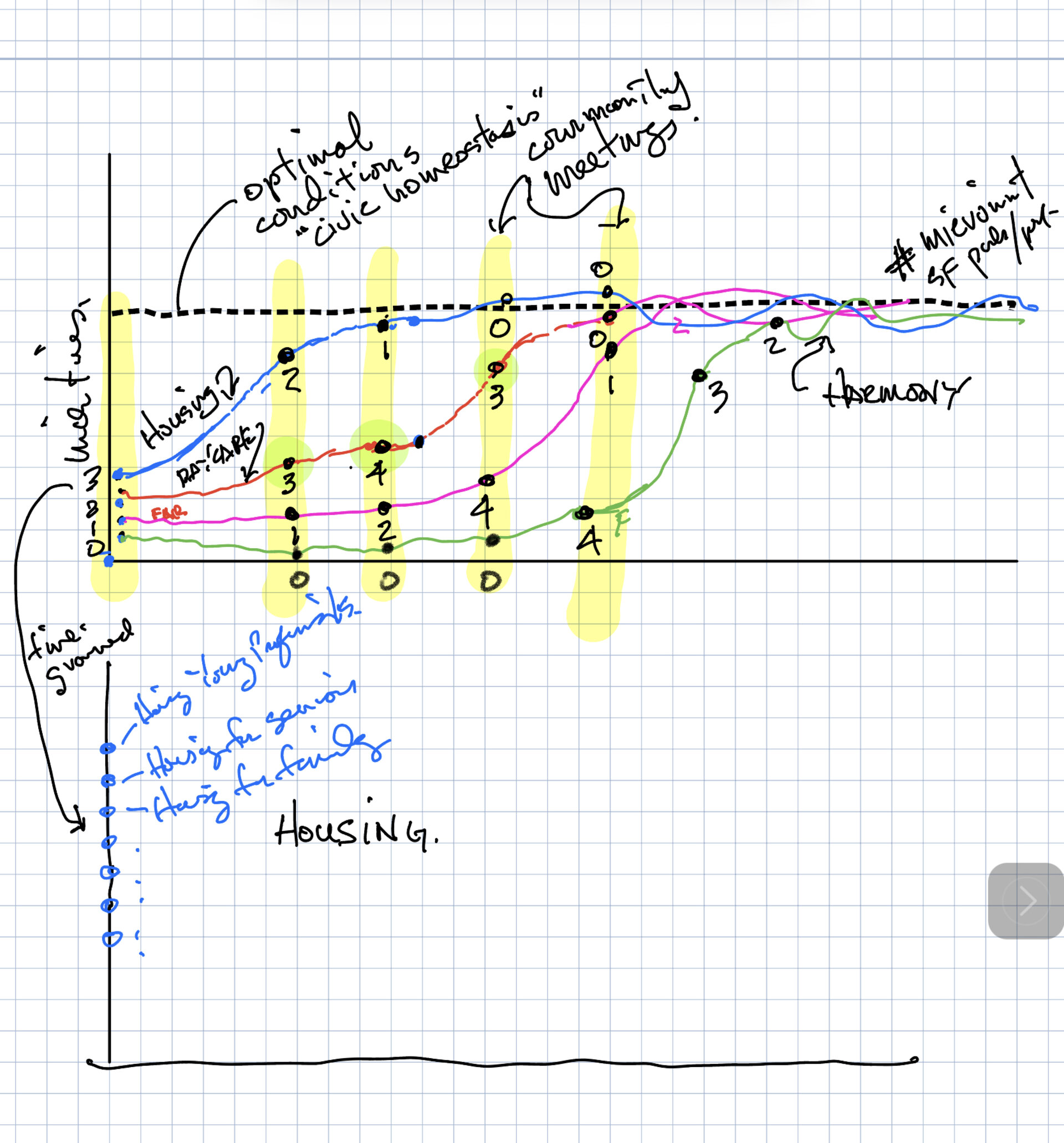
two step approval process
- high level: land use prioritization
- different levels: ’residential’ vs ’affordable housing’
- individual projects: developer have the ’FAR slider’
the voting mechianism -> use turnout or similar methods developed by previous efforts
Cities:Skylines
How would we simulate the process?
Using Cities:Skylines as an example. This is what the game aready have.
- objective
The games basic objective is to have more population. Although players have other personal aesthetic goals.
- we have a demand
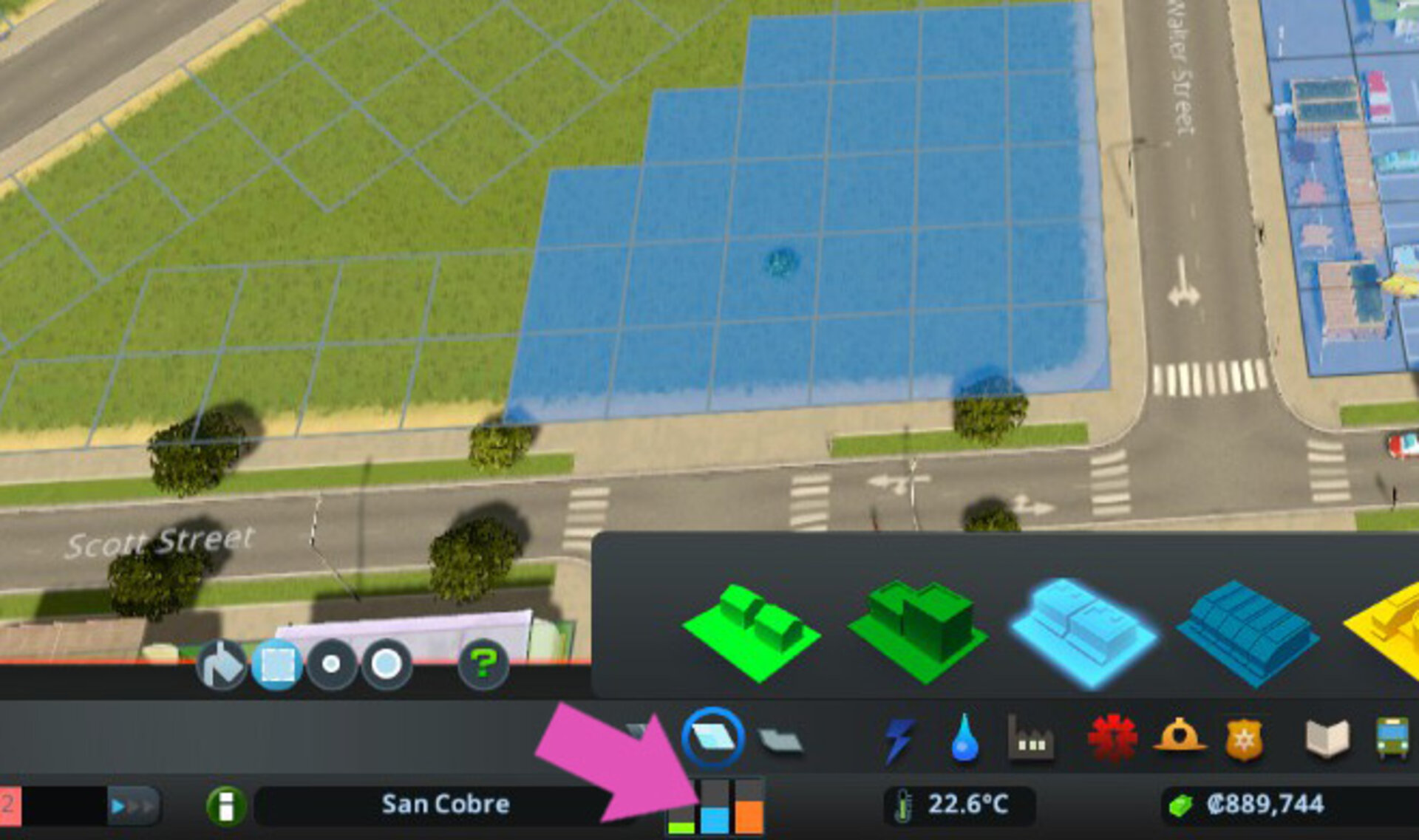
| green | blue | orange |
| residential | commercial | industrial/office |
Players change the zoning to meet the demand. Areas that are zoned in high demand landuse will get filled faster.
- statistics
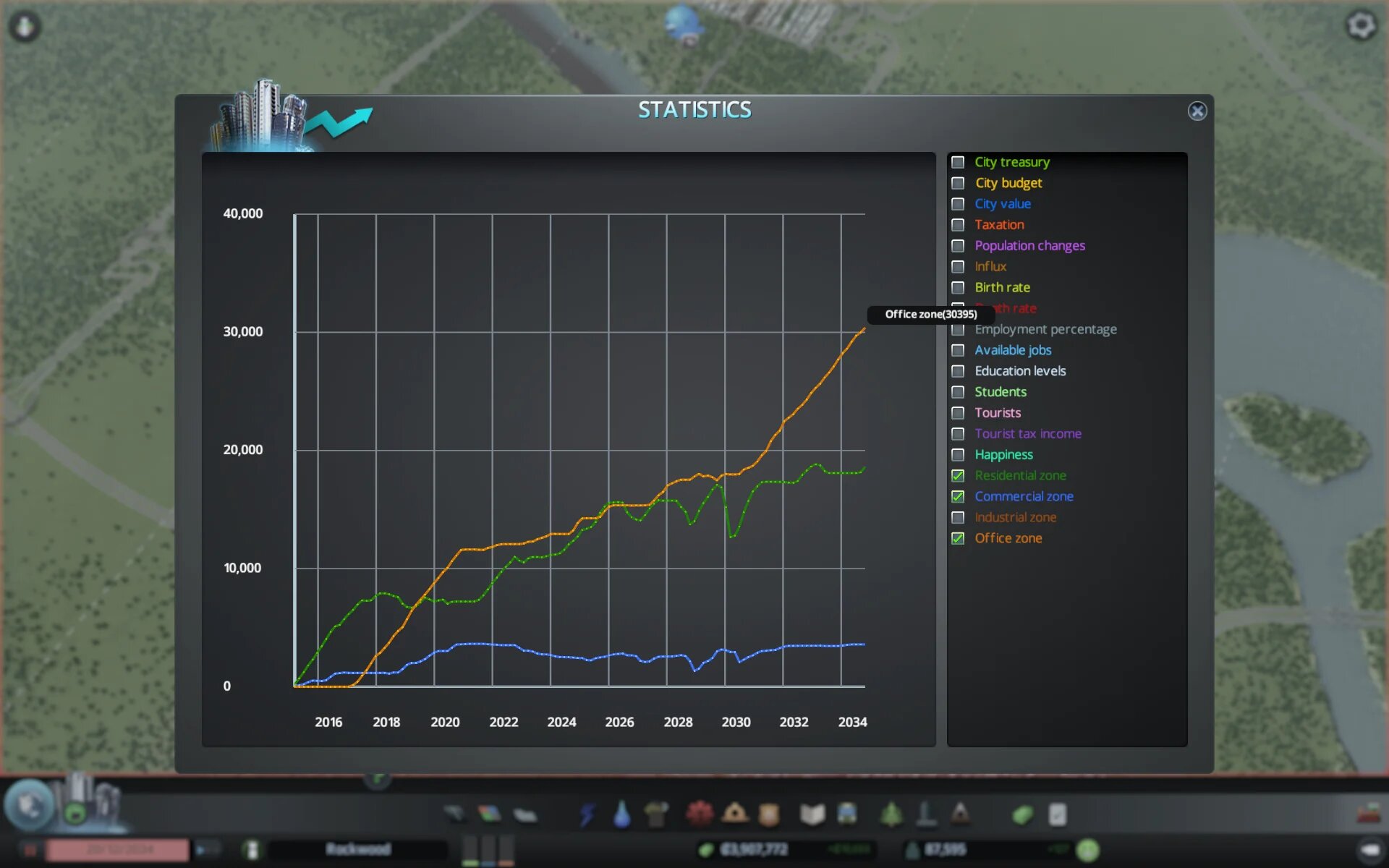
Figure 1: Cities:Skyline statistics
difference
- Demand is provided by the simulation. In real life you will need analysis procedures for market trend. Individual projects face nearby citiezens response in the process. In algoritmic zoning, we gauge this by the high level prioritization.
- Once you assign landuse, wheather or not it will get developed is purely in accordance with the demand. Obiously, there is no incentive mechanism for the devlopers to get additional (profitable) floor area. Also, if a buidling (not limited to the buildings defined zoning types) gets built, generally it will affect the nearby ’happieness’ of citizens. There is no way to convert that money or compensation.
-> player is indirectly playing the developers side, since A) this will lead to more citizens (pop increase), B) this inturn will generate more tax revenue to futher develop the cities infrastructure.
homeostasis
For example we have to two types of amenities, a grocery store and a park.
\[ u = \sqrt{n} \]
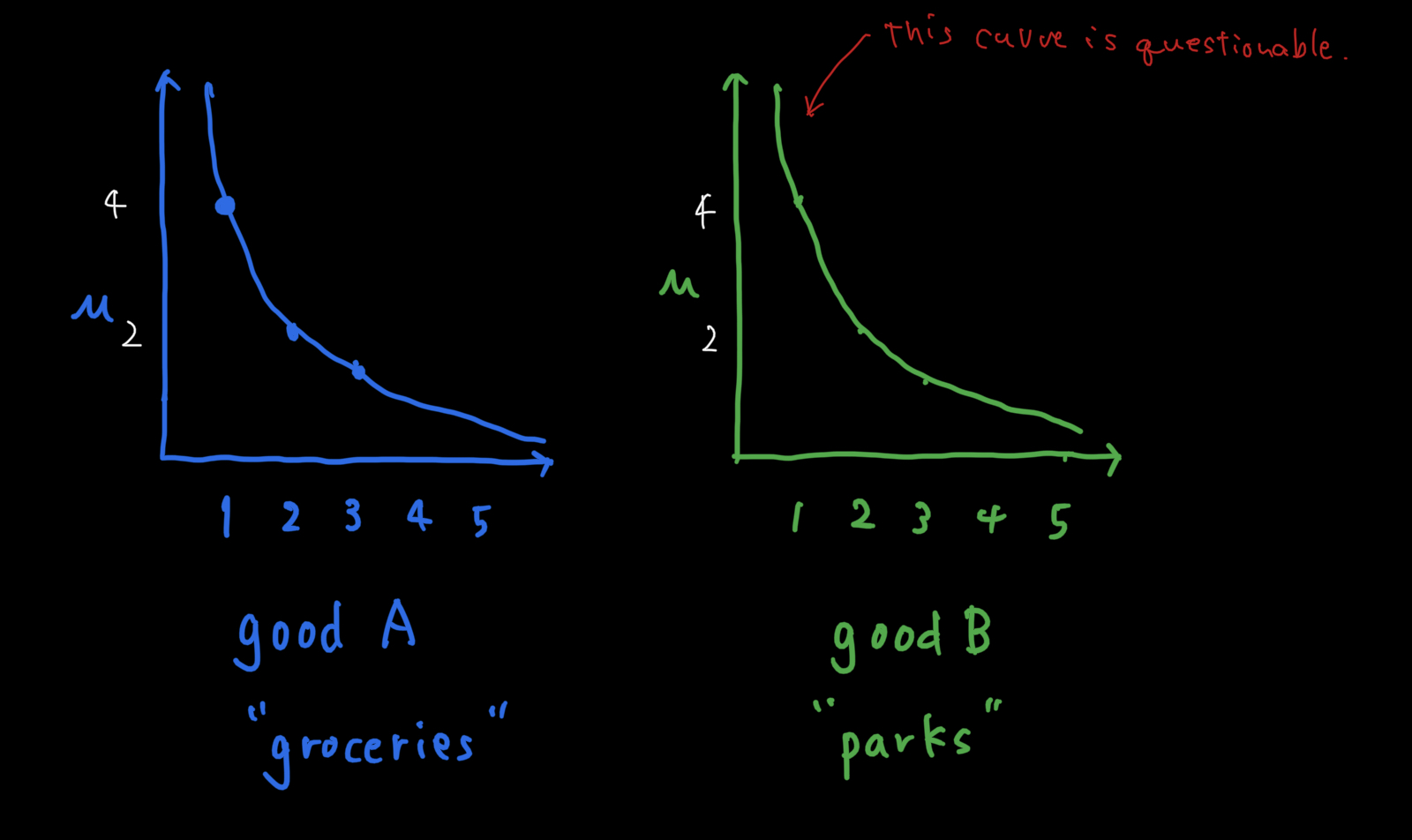
If we have two grocery stores the sum of the utility will be 4 + 2 = 6, since the second grocery will be less appriciated. Instead, if we have one each, the sum of the utility will be 8 (4 + 4)
Higher diversity in amenities are better.
substitutional goods and complementary goods
when looking into the relation of two goods, some are complementary and some are substitutional.
so, depending on how people think a is better than b the utility might have impact.
IRV vs pair wise comparison
IRV is one method of counting votes, where the caculation is recursive. take the folloing example, when five people are choosing from three amenity options.
| alice | bob | charlie | david | eva |
| park | book store | police sta. | park | police sta. |
| book | park | park | book | book |
| police | police | book | police | park |
first round
we get the following result
| park | book store | police station |
| 2 | 1 | 2 |
none of them got the majority, we step further into the second round, by eliminating the least favorable option, in this case book store.
second round
we get winner since, bob’s first preference was crossed out, and park earns another point.
| park | book store | police station |
| 3 | 0 | 2 |
for this irv, we might naturally conclude that we want a police station after a park.
pair wise doesn’t conform
if we compare two goods in isolation, we get the following trend:
| park > book | 3 |
| park > police | 3 |
| book > police | 3 |
the top two lines does not contradict with irv’s result. yet this shows that a book store is actually perferable than a police station. you can see the irv shows different results if you eliminate park and do the recusive calculation over again.
quadratic voting
the initial intent of quadratic voting (qv) is to be able to show different levels of opinion. some migh argue that 1p1v is not fair when someone have stronger opinions that another. which deincentivises to be a professional. in our case we can convert the stronger opinion to for example, distance. if alice lives close than bob to the prospective landfill site, she should have a stronger say about the topic. The question is how strong should it be? It might be qudratic, but this needs mathemtical proofing and revisit the reasoning behind taking the square root.